2進数表示 (bin)
>>> bin(23)
'0b10111'16進数表示 (hex)
>>> hex(121)
'0x79'
>>> hex(300)
'0x12c'ビット演算
論理積 (&)
>>> a = 22
>>> bin(a)
'0b10110'
>>> b = 19
>>> bin(b)
'0b10011'
>>> a & b
18
>>> bin(a & b)
'0b10010'論理和 (|)
>>> a = 20
>>> b = 10
>>> bin(a)
'0b10100'
>>> bin(b)
'0b1010'
>>> a | b
30
>>> bin(a | b)
'0b11110'排他的論理和 (^)
>>> a = 25
>>> b = 10
>>> bin(a)
'0b11001'
>>> bin(b)
'0b1010'
>>> a ^ b
19
>>> bin(a ^ b)
'0b10011'ビット反転 (~)
ビット反転結果は元の数の1の補数(減基数の補数)と同じになる。(1の補数は元の数に足して桁上がりを起こさない最大の数)
4ビットで桁上がりをしないためには、加算して1111になるように元の数の各桁が1ならば0、0ならば1と反転すればよいので、結局ビット反転することと同じになる。
0100(4) + 1011(11) = 1111(15)
この場合、1011より1多いと桁上がりして10000となるので、0100に足して桁上がりを起こさない最大の数は1011。また、1011より1多い1100は桁上がりする最小の数なので0100の2の補数。
このように、1の補数は2の補数より1少ない。そこで元の値をxとすると、xの2の補数は-xなので、1の補数はそれより1少ない-x-1となる。~xはxの1の補数と同じなので、~xも-x-1 = -(x+1)となる値を返す。
>>> a = 27
>>> bin(a)
'0b11011'
>>> b = ~a
>>> bin(b)
'-0b11100'
>>> ~b
27
>>> b
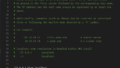
-28ビットシフト (<<, >>)
>>> a = 10
>>> bin(10)
'0b1010'
>>> bin(a << 2)
'0b101000'
>>> bin(a >> 1)
'0b101'

コメント